[最も共有された! √] 5−2 320069

Example 18 Solve 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Examples
Example 4x x 2 − 3x 5 − 2 How Many of The Roots are Positive?5−2 = 3 × multiply 4×3 = 12 ÷ divide ÷5 = 4 / divide /5 = 4 ( ) grouping symbols 2(a−3) grouping symbols 2 a−3(bc) { } set symbols {1, 2, 3} π pi A = π r 2 ∞ infinity ∞ is endless = equals 11 = 2 approximately equal to π 314 ≠ not equal to
5−2
5−2-27 SIMPLIFYING RADICALS Simplest form Similar radicals 2nd level Simplifying the square roots of powers Fractional radicand W E SAY THAT A SQUARE ROOT RADICAL is simplified, or in its simplest form, when the radicand has no square factors A radical is also in simplest form when the radicand is not a fraction Example 1Examples 14 1 Let X = Y = the set of real numbers, and let f be the squaring function, f x → x2 The range of f is the set of nonnegative real numbers;
Math Temple Edu
First, rewrite the polynomial from highest to lowest exponent (ignore any "zero" terms, so it does not matter that x 4 and x 3 are missing) −3x 5 x 2 4x − 2 Then, count how many times there is a change of sign (from plus to minus, or minus to plus)Joe Foster Integration by Partial Fractions Summary Method of Partial Fractions when f(x) g(x) is proper (degf(x) < degg(x))1 Let x−r be a linear factor of g(x)Suppose that (x−r)m is the highest power of x−r that divides g(x)Then, to this factor, assign the sum of the m partial fractions A1 (x −r) (x −r)2A3 (x −r)3A23/5/21 This article was coauthored by wikiHow StaffOur trained team of editors and researchers validate articles for accuracy and comprehensiveness wikiHow's Content Management Team carefully monitors the work from our editorial staff to ensure that each article is backed by trusted research and meets our high quality standards This article has been viewed 43,871 times
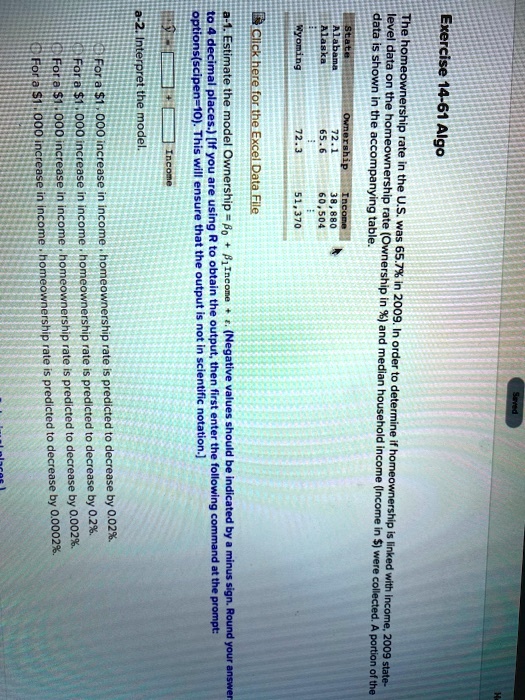
No negative number is in the range of this function 2 Consider a university with 25,000 students Let X be the students enrolled in the university, let Y be the set of 4decimal place numbers to , and let f
5−2のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「5−2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「5−2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「5−2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「5−2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「5−2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「5−2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「5−2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「5−2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「5−2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「5−2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「5−2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
コメント
コメントを投稿